

Supercells

Supercell is a widely used crystallographic concept ¹. A general theoretical background is offered in the expandable section below for the readers unfamiliar with the topic. The rest of this documentation page explains how supercell generation is implemented in the Materials Designer interface.

Theoretical Background

What are supercells?

A material has a crystal structure associated with it and the latter is described by a unit cell. There are an infinite number of unit cells U with different shapes and sizes which can describe the same crystal. The supercell S of unit cell U is defined as a cell which describes the same crystal, but has larger volume than cell U ¹.

2D examples

Examples of different supercells for the same underlying 2D cubic crystal are shown in the figure below. The relatively large size of such supercells has to be compared to the smaller surface area of the most basic (primitive) unit cell of this crystal containing just one lattice point, example of which is shown towards the center of the figure. Both diagonal and non-diagonal supercells are included in this picture to reflect the general scope of the supercell definition.

Why are supercells useful?

There are many instances where the construction of supercells affords for an easier ascertainment of useful crystal properties and visual symmetric qualities, which could otherwise be difficult to determine by looking at just the initial cell.

Phonon calculations

There are many occurrences of methods in computational materials science for determining crystal structure properties which rely on small perturbations of the supercells away from their original equilibrium configurations. For example, during phonon calculations by the small displacement method ("frozen phonon"), the frequencies are calculated using the finite force values computed on slightly displaced atoms in a supercell of the original structure.

Conventional vs primitive cells

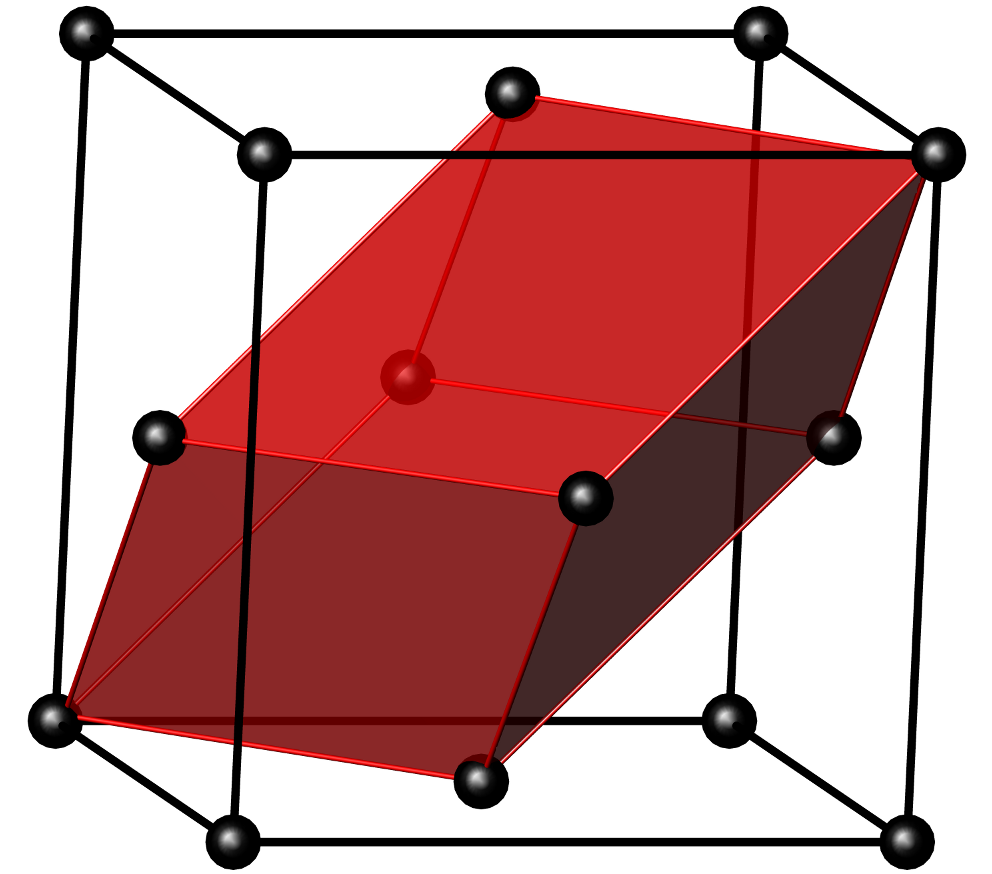
The conventional cells of body-centered (bcc) or face-centered (fcc) cubic crystals, containing two atoms and four atoms respectively, reflect more intuitively the overall symmetry of such systems. The figure below illustrates this for the example of an fcc lattice. In this image, the volume marked in red represents the primitive unit cell, whereas the over-arching cubic conventional supercell exhibits the full face-centered cubic symmetry from which the corresponding crystal structure gets its name:

Defects

Finally, supercells are also commonly used in computational models of crystal defects, in order to allow for the use of periodic boundary conditions.

How are supercells defined?

The basis vectors of unit cell U $({\vec {a}},{\vec {b}},{\vec {c}})$ can be transformed to basis vectors of supercell S $({\vec {a}}',{\vec {b}}',{\vec {c}}')$ by way of the following linear transformation:

$${\displaystyle {\begin{pmatrix}{\vec {a}}'&{\vec {b}}'&{\vec {c}}'\\\end{pmatrix}}={\begin{pmatrix}{\vec {a}}&{\vec {b}}&{\vec {c}}\\\end{pmatrix}}{\hat {P}}={\begin{pmatrix}{\vec {a}}&{\vec {b}}&{\vec {c}}\\\end{pmatrix}}{\begin{pmatrix}P_{11}&P_{12}&P_{13}\\P_{21}&P_{22}&P_{23}\\P_{31}&P_{32}&P_{33}\\\end{pmatrix}}}$$

where ${\hat {P}}$ is the corresponding linear transformation matrix. All items $P_{ij}$ should be integer numbers, and it is furthermore required that $\det({\hat {P}})>1$ (with $\det({\hat {P}})=1$ the transformation preserves the volume of the original unit cell). For example, the matrix

$${\displaystyle P_{P\rightarrow I}={\begin{pmatrix}0&1&1\\1&0&1\\1&1&0\\\end{pmatrix}}}$$

transforms the primitive cell of a body-centered cubic lattice to its fully-symmetric conventional unit cell.

Another particular case of the transformation is a diagonal form $P_{i\neq j}=0$ of the matrix. This type of transformation is referred to as diagonal supercell expansion, and can be interpreted as a simple repetition of the initial cell over its crystallographic axes.

The Generate Dialog

Choose the Supercell option in the Advanced menu to opend the "Supercell Generation Dialog".

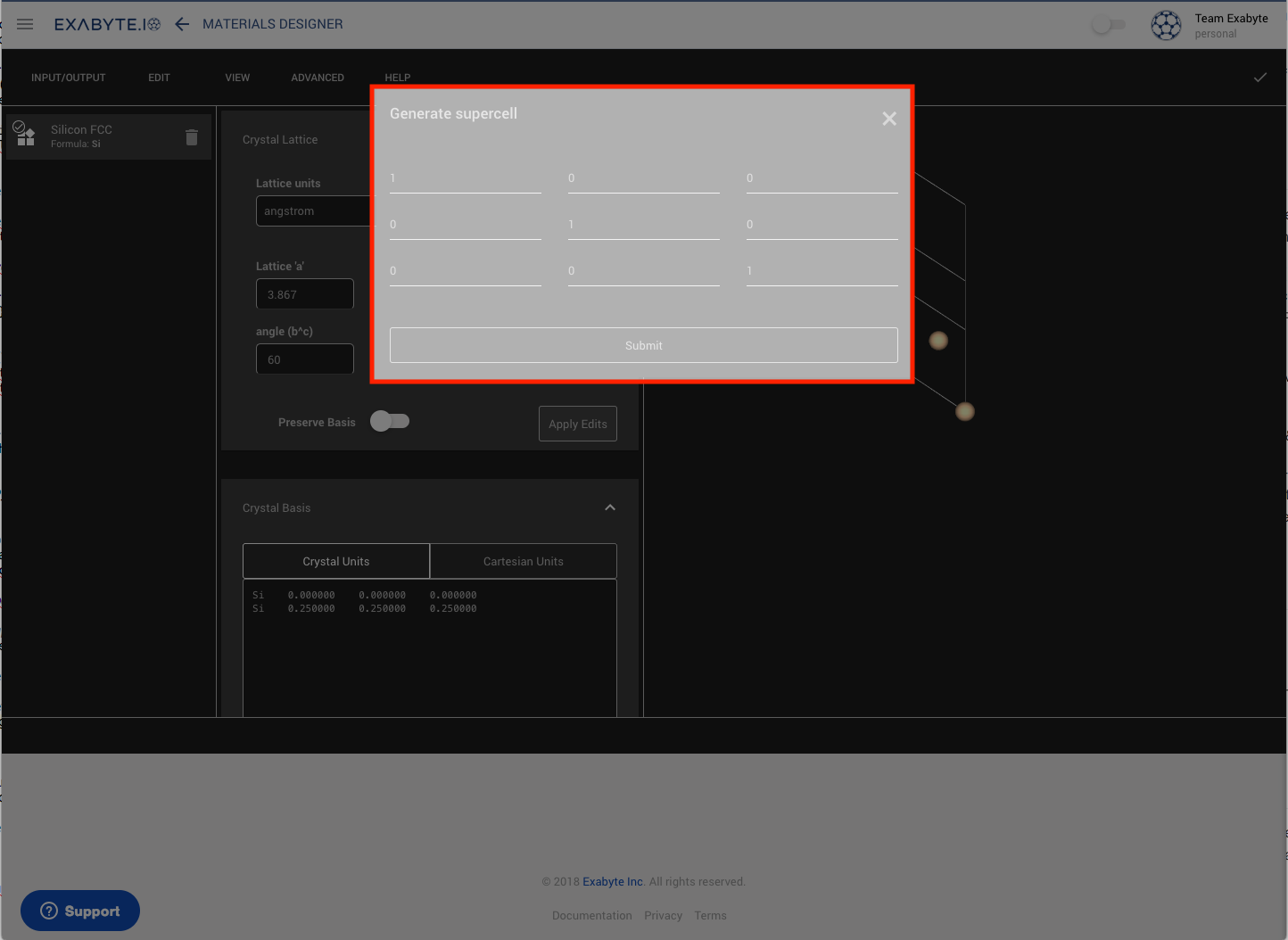
Supercell Transformation Matrix

The overlay, highlighted in the image below, will allow the reader to set the parameters of the supercell transformation matrix (with its elements positioned exactly as explained in the previous paragraph).

Generate Supercell

When finished setting up the transformation matrix, click Submit button and both the crystal data and the 3D representation will update accordingly to reflect the newly-generated supercell.

Animation

Click on the animation below to see the above in action. In this example, we generate a 2 x 2 x 2 supercell of a cubic structure containing two atoms by inserting the diagonal elements of the corresponding transformation matrix, whilst leaving the off-diagonal elements to zero.

Links

---

1. Wikipedia Supercells, Website ↩↩