

Phonon Dispersions and Density of States Calculation on Grid¶

This tutorial page explains how to calculate the Phonon Dispersion Curves and Phonon Density of States of materials based on Density Functional Theory. We will be studying crystalline Silicon in the standard cubic-diamond crystal structure, and we will use Quantum ESPRESSO as our simulation engine.

Quantum ESPRESSO version considered in this tutorial

The present tutorial is written for Quantum ESPRESSO at versions 5.2.1, 5.4.0, 6.0.0 or 6.3.

What sets the present tutorial apart from the other tutorial on phonon calculations is the employment of the "Grid Method" for computing the vibrational properties of materials, which is reviewed in the subsequent paragraph. This method is based on a map type workflow, where multiple branches are executed in parallel as separate independent Jobs, with the consequent gain in computational efficiency and overall speed of the phonon calculation. More information on this method, together with a demonstration of its application and results on a sample set of materials, can be found in Ref. ¹.

The Grid Method for Phonon Calculations¶

The Grid Method allows for an efficient parallelization of the tasks for calculating the individual vibrational modes. This method optimizes the corresponding workflow in order to obtain the frequencies for each individual symmetry-irreducible representation ² of the phonon lattice perturbations in parallel.

Steps Involved in Grid Method¶

We thus implement a grid-parallel workflow for the calculation of the phonon dynamical matrices, initially explained in the first reference cited in this page. During the actual phonon calculation part of the workflow, the following steps happen:

First, the irreducible representations for the vibrational modes (irreps) are generated, based on the sampling grid in the reciprocal space (q-point grid).
Second, a separate calculation is prepared and submitted for execution in parallel for each pair or irreducible representation and q-point, via the implementation of a Map for performing a distributed calculation ("map" stage).
Finally, after the calculations for all irreps-q points pairs are finished, the dynamical matrices are collected and aggregated together, and phonon dispersions and density of states are calculated ("reduce" stage).

Thus, we employ a "map-reduce" general type of logic and scenario within the overall workflow, where the individual calculation tasks are performed independently and in parallel with one another. This allows for an improved efficiency and speedup of phonon calculations compared to the more traditional serial approach, such that the limiting factor within the overall calculation is the longest run per individual irreducible representation-q point pair.

Schematic Visualization of Grid Method¶

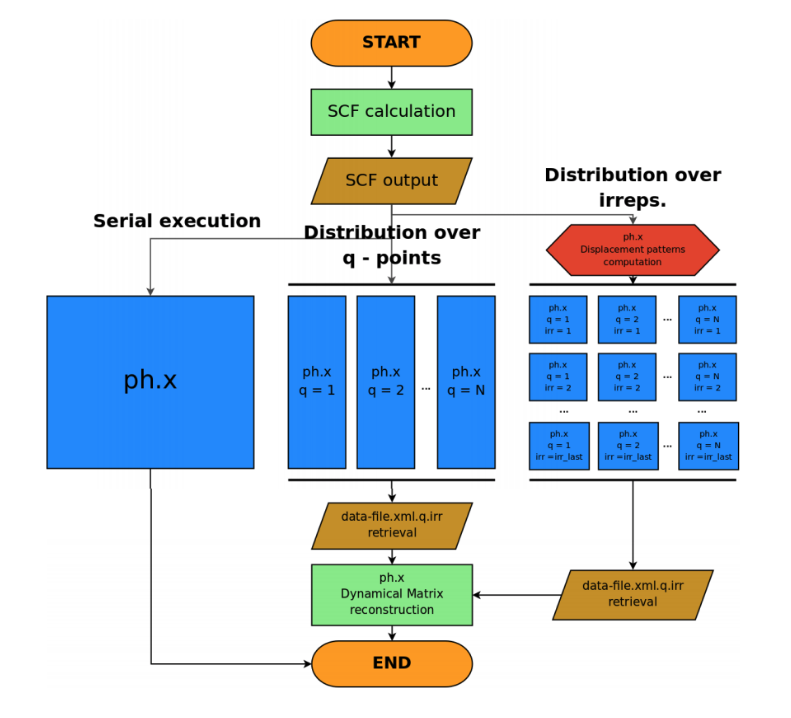
A schematic summary of the above workflow procedure is offered in the figure below. This flowchart depicts all different approaches to the calculation of the phonon dispersions and lattice vibrations. The approach used in the present tutorial is the rightmost one. Here, ”SCF” stands for the self consistent field preliminary calculation, ”ph.x” denotes the phonon calculations by means of Density Functional Perturbation Theory, and "irrep" is an irreducible representation of a vibrational phonon mode.

phonons grid method

Workflow Structure¶

We review now the different steps involved in implementing the above general Grid Phonon theoretical framework in an actual Workflow deployable on our platform. We shall consider the example case of the Quantum ESPRESSO modeling engine.

1. Preliminary SCF Calculation¶

The first subworkflow step in the overall "Phonons Grid" Workflow is a standard self-consistent field (scf) total energy calculation, providing the ensuing steps of the workflow with the wavefunctions of the material structure under investigation.

For the sake of this example, we can set the grid of special k-points to 6 x 6 x 6, under Important Settings.

2. Q-points and Irrep Generation¶

The second subworkflow step ("ph-init-qpoints") is composed of a single unit, which consists in generating the grid of q-points over which the vibrational phonon modes calculations will be performed, for each irreducible representation of such modes.

The size of this q-grid should be a divisor of the size of the above-mentioned k-grid. Hence, a q-grid of 2 x 2 x 2 should suffice in this case, which can be set under Important Settings.

3. Extraction of q-points/irrep pairs¶

The "espresso-xml-get-qpt-irr" subworkflow comprises a main python script, whose role is to parse and extract q-points and irreducible representations from the previously-generated Quantum ESPRESSO XML data. Each distinct combination of q-point and irrep is added as a separate entry to what follows.

4. Map Distributed Phonon Calculation¶

The ensuing subworkflow consists in the Map for performing the distributed parallel phonon calculations across each q-point/irrep pair extracted previously. The list of q-points/irrep pairs can be inspected under the "Data" tab of the Map editor interface.

Care should be taken to set the q-grid under the "Important Settings" of the "ph-single-irr-qpt" map subworkflow again to 2 x 2 x 2, as in the previous steps.

5. Reduce and Aggregate Results¶

The final "Reduce" subworkflow collects together the results of the previous calculations over each independent q-point/irrep pair, via the "ph_grid_restart" unit. Here, the size of the q-grid under Important Settings should once again be set to the 2 x 2 x 2 value being considered in the present example.

These combined results are then used to complete the phonon dispersion and density of states calculation, through the help of the Quantum ESPRESSO "q2r" and "matdyn" executables.

Creating and Executing Job¶

"Phonon Map" workflows can readily be imported into the account-owned collection from the Workflows Bank.

Apart from this, the same procedural instructions as in the other phonons calculation tutorial should be followed for creating and launching the corresponding grid-based phonon Job through our Web Interface, and for inspecting the associated results.

Animation¶

In the video animation below, we outline the procedure for creating and executing a phonon calculation job via the Grid Method. We conclude by inspecting the corresponding results for the Phonon Dispersion Curves and Density of States, considering crystalline silicon as our demonstrative sample operated in conjunction with the Quantum ESPRESSO simulation engine.

Computational cost of phonon calculation

Phonon calculations are in general quite computationally demanding. We therefore recommend the employment of at least 8 computing cores. For larger calculations, OF queues will have faster turnaround than the OR queues considered in the video.