Stress Tensor¶
Non-Scalar Mechanical
The stress tensor {\boldsymbol {\sigma }} 1 is a Physical property. It is a second-rank tensor, representable as a Matrix, which consists of nine components \sigma _{ij} that completely define the state of stress at a point inside a deformed material.
{\boldsymbol {\sigma }}=\left[{{\begin{matrix}\sigma _{{xx}}&\sigma _{{xy}}&\sigma _{{xz}}\\\sigma _{{yx}}&\sigma _{{yy}}&\sigma _{{yz}}\\\sigma _{{zx}}&\sigma _{{zy}}&\sigma _{{zz}}\\\end{matrix}}}\right]
The image below offers an explanation of the directions in which each shear and normal stress component expressed above acts upon, relative to a Cartesian coordinate system.
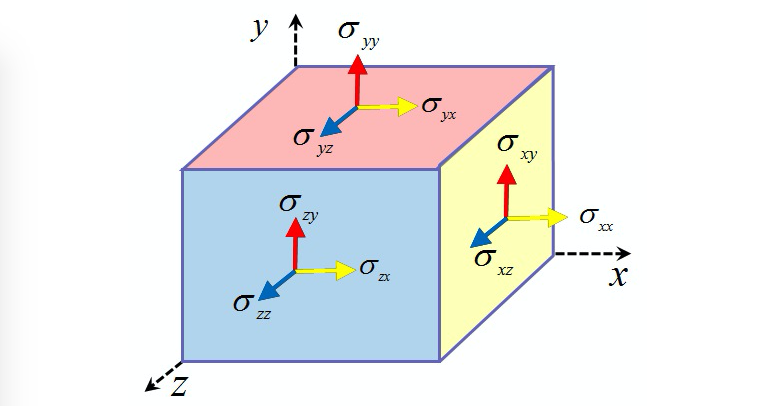
Example¶
Under the Results Tab of Job Viewer, the components of the stress tensor are presented as follows, expressed in units of kilobars (kbar).

Schema¶
The JSON schema and an example representation for this property can be found here.