

K-point Convergence

We consider the case of convergence based on the study of the number of sampling points (k-points) in the reciprocal cell.

In most cases, in order to achieve the desired precision, the total energy should not increase significantly when the k-point density is increased.

Algorithm

The flowchart of the optimization algorithm used to find the optimal density is presented below.

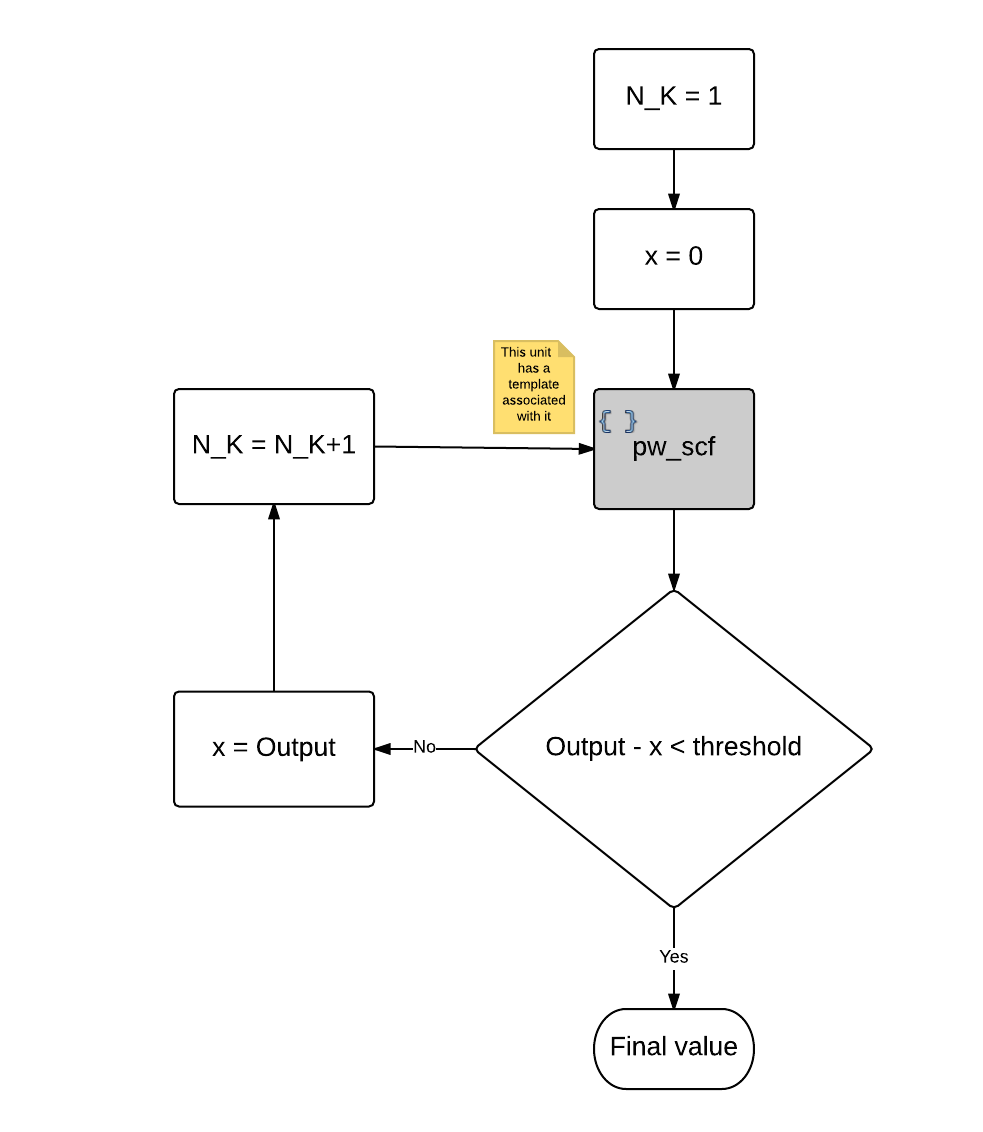
Here, we use a uniform k-point mesh (same in each of the three spatial directions), and first initiate the number of kpoints N_K at 1. We then run a self-consistent density functional theory calculation (pw_scf - using Quantum ESPRESSO's terminology), and check whether the Output value difference at current step and at previous one (x) is less than the convergence threshold. This whole process is repeated over a certain number of iterations.

Currently, the default k-point convergence algorithm systematically increments the starting k-point density by 1 in along each reciprocal lattice vector, until the total energy of the system does not increase by more than 0.001% (10^-5).

Properties Sensitive to Convergence

Some properties, especially those depending on atomic forces, derivatives of the total energy, and displacements or perturbations, are highly dependent upon the quality of convergence and relaxation. For example, accurate calculation of zero point energy requires a well converged k-point grid to sample the total energy space when atoms are displaced from their equilibrium positions.

Animation

In the following animation, we show how to insert a k-point convergence add-on to a total energy subworkflow, from the Actions Menu in Workflow Designer. The new compute units are consequently added to the subworkflow.

Please see the k-point convergence tutorial for more details.