

Setting the Crystal Basis¶

The atomic basis of a Material's crystal structure can be edited and set by expanding the "Crystal Basis" section in the central panel of the Materials Designer interface. The appearance of the "Crystal Basis" editor within the wider interface is shown in the figure below:

Setting the Crystal Basis

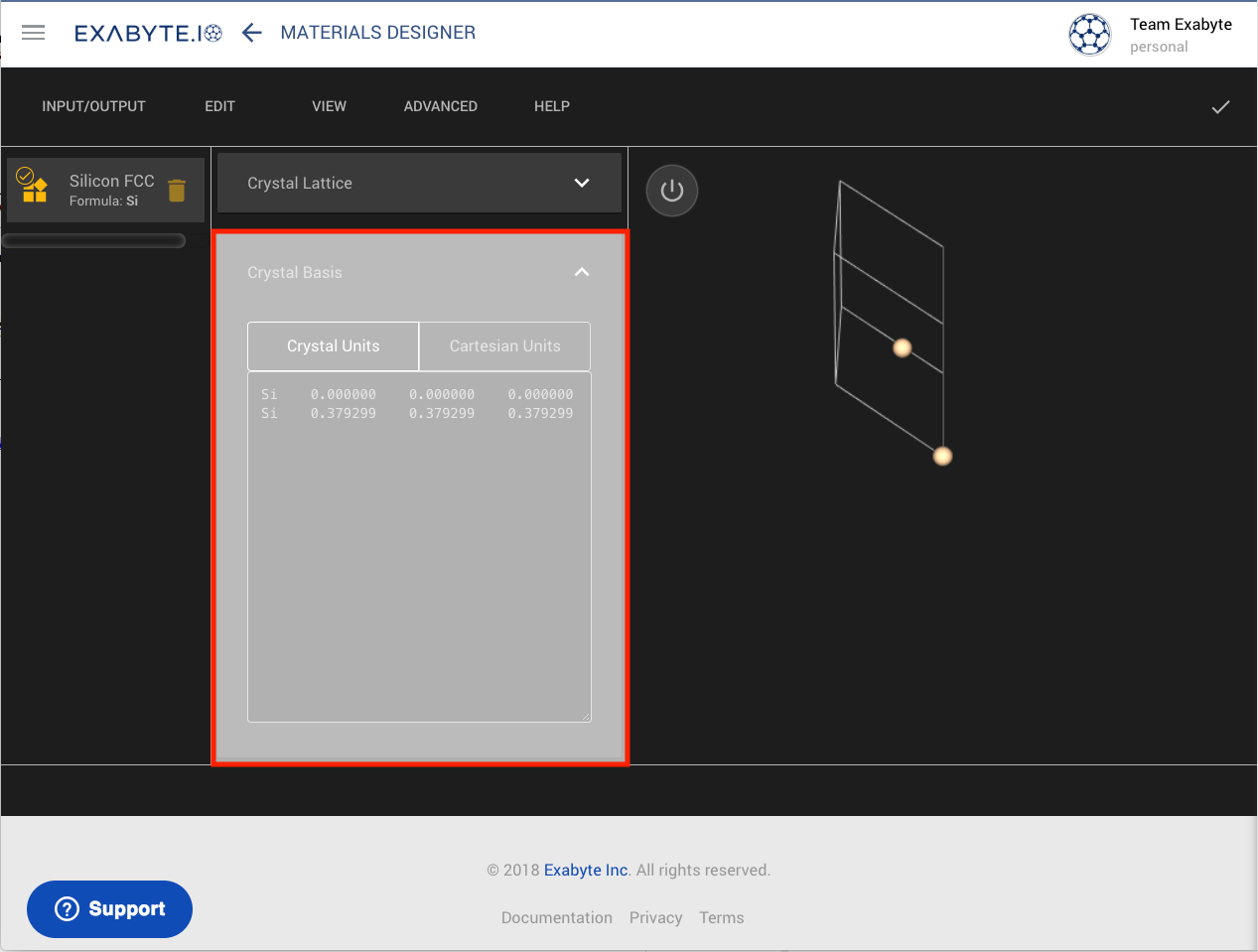
Coordinate Units¶

XYZ file format¶

Crystal Basis source can be edited directly as text. You may edit the elements' chemical symbols and coordinates directly inside the corresponding area, and the changes will be reflected in real-time (after clicking outside of the text area).

The data has to be entered according to the "XYZ" format for defining crystallographic structural information ¹. The initial line specifying the total number of atoms is omitted. Some example lines for defining the pyridine molecule following this format are given below:

C       -0.180226841      0.360945118     -1.120304970
C       -0.180226841      1.559292118     -0.407860970
C       -0.180226841      1.503191118      0.986935030
N       -0.180226841      0.360945118      1.685965030
C       -0.180226841     -0.781300882      0.986935030
C       -0.180226841     -0.837401882     -0.407860970
H       -0.180226841      0.360945118     -2.206546970
H       -0.180226841      2.517950118     -0.917077970
H       -0.180226841      2.421289118      1.572099030
H       -0.180226841     -1.699398882      1.572099030
H       -0.180226841     -1.796059882     -0.917077970

Coordinate units: Crystal and Cartesian¶

The default representation of the atomic coordinates is in crystal units (also commonly called fractional) ². In this coordinate system, the axes of the unit cell are used as the basis vectors to describe the positions of the atoms.

In addition, the atomic coordinates can be converted from such crystal units to a standard orthogonal Cartesian reference system (expressed in units of Angstroms) by clicking on "Cartesian Units".

Transformation between Crystal and Cartesian units¶

Expand to view ...

If we define the unit cell of the crystal as a parallelepiped characterized by the lengths of its edges $a$ , $b$ , $c$ (expressed in Angstroms) and angles between them $\alpha$ , $\beta$ , $\gamma$ , then the transformation equation for converting a generic set of crystal coordinates $(u,v,w)$ to its corresponding Cartesian Angstrom coordinates $(x,y,z)$ can be expressed as:

$\left[{\begin{matrix}x\\y\\z\end{matrix}}\right]=\left[{\begin{matrix}a&b\cos(\gamma )&c\cos(\beta )\\0&b\sin(\gamma )&c{\frac {\cos(\alpha )-\cos(\beta )\cos(\gamma )}{\sin(\gamma )}}\\0&0&{\frac {\Omega }{ab\sin(\gamma )}}\end{matrix}}\right]\left[{\begin{matrix}u\\v\\w\end{matrix}}\right].$

The inverse procedure can be achieved through:

$\left[{\begin{matrix}u\\v\\w\end{matrix}}\right]=\left[{\begin{matrix}{\frac {1}{a}}&-{\frac {\cos(\gamma )}{a\sin(\gamma )}}&bc{\frac {\cos(\alpha )\cos(\gamma )-\cos(\beta )}{\Omega \sin(\gamma )}}\\0&{\frac {1}{b\sin(\gamma )}}&ac{\frac {\cos(\beta )\cos(\gamma )-\cos(\alpha )}{\Omega \sin(\gamma )}}\\0&0&{\frac {ab\sin(\gamma )}{\Omega }}\end{matrix}}\right]\left[{\begin{matrix}x\\y\\z\end{matrix}}\right]$

Animation¶

Click on the animation below to see the above in action. Here, we change the x-axis coordinate of the second off-origin atom in the two-atom basis of Silicon, and then convert these new modified coordinates to Cartesian units.

Non-Periodic Basis Transformations¶

When Edit - Toggle "isNonPeriodic" is used, the basis of the structure will automatically be converted to Cartesian Coordinates and translated to the center of the lattice. This is done by translating each basis coordinate so that the center of coordinates for the structure and the center point of the lattice align.

Toggle "isNonPeriodic" Animation¶

Click on the animation below to see the **Toggle "isNonPeriodic" button in action.